Abstract
We introduce the concept of Fully Homomorphic Encryption (FHE) Rollups: a more scalable technique for executing arbitrary confidential smart contracts. Recent works [1, 16, 39] have shown that FHE is a viable solution for adding confidentiality to smart contracts. However, these works limit scalability as they require all nodes in the network to execute FHE computations and reach consensus over the encrypted state.
Inspired by the recent movement towards layer-2 solutions in the Ethereum ecosystem, we present the first rollup based FHE architecture. We argue that while for plaintext computation rollups are a needed solution, in the context of FHE, where the computational overhead is orders of magnitude higher, they are a necessity.
In our design, we take an optimistic rollup approach, allowing us to avoid the orders of magnitude penalty incurred by state-of-the-art verifiable FHE techniques [43]. In fact, our framework can be seen as a cryptoeconomic solution to solve the same problem.
Focusing on the Ethereum ecosystem, we present and overcome the challenge of the base-layer arbitrating nonEVM native fraud proofs. We achieve this without requiring any changes to Ethereum, showing that native FHE rollups on Ethereum are indeed possible. We build a partial proofof-concept that demonstrates this using Arbitrum’s Nitro prover and Zama’s tfhe-rs libraries.
1. Introduction
Preface: This is the first release (v0.1) of Fhenix’s ’Rolling Whitepaper’ on FHE Rollups. It is meant to be a breathing document we update and expand on on a rolling basis, including incorporating feedback from our growing community, as well as external researchers.
Blockchains ensure correct execution and censorship resistance in a trust-minimized way (i.e., without trusting any centralized operator), at the expense of data confidentiality. Inherently, all data on-chain is public, because all nodes need to see the data to reach consensus. Despite popular belief, this extreme level of transparency is a by-product and not a goal of the system, and it greatly.limits the type of use-cases we can build, since we cannot build any application that needs to utilize sensitive data.
In recent years, researchers and practitioners have employed several privacy-preserving technologies to solve the problem of confidentiality on the blockchain, in a body of work that became to be known as confidential smart contracts (e.g., [2, 13, 38, 39, 48, 49]). Of all these techniques, Fully Homomorphic Encryption (FHE) is perhaps the most ambitious, as it allows to directly compute over encrypted data without decrypting it. FHE has improved by leaps and bounds since Gentry presented the first construct almost a decade and a half ago [19]. Still, FHE requires significant computational overhead compared to computing in plaintext, making it impractical for execution at the Layer 1 (L1) level where every node is required to replicate the entire computation, which is the approach that state-of-the-art FHE-based confidential smart contracts frameworks are taking [1, 39]. Inspired by the recent movement towards layer-2 solutions in the Ethereum ecosystem [26, 35, 36], we present the first architecture of an FHE-based rollup. We argue that while for plaintext computation rollups are a needed solution, in the context of FHE, where the computational overhead is orders of magnitude higher, they are a necessity. In a rollup architecture, smart contract execution (the heavy-duty part of validating blocks) is separated from verifying the execution and reaching consensus. This ensures that only a single node (or a small number of nodes) are actually doing the computational heavy lifting, without reducing security. Furthermore, this node can be vertically (and horizontally) scaled as needed, including utilizing more expensive specialized hardware (GPUs, ASICs). The latter is common with zero-knowledge (zk) based rollups 1 , which like FHE also leverages computationally-intensive cryptography, and can be leveraged in much the same way for FHE computations. However, in our design, we take an optimistic rollup approach as opposed to a zk-rollup approach, allowing us to avoid the orders of magnitude penalty incurred by state-ofthe-art verifiable FHE techniques [43]. In fact, our framework can be seen as a cryptoeconomic solution to solve the same problem.
____________________________________________
1 e.g., https://www.ingonyama.com, https://www.risczero.com
1.1 Our contributions In this paper, we make the following main contributions:
• We introduce Fhenix, the first layer-2 confidential smart contracts platform, enabling greater efficiency and scalability.
• We demonstrate through a proof-of-concept implementation, that an optimistic FHE rollup can be built on top of Ethereum, without making any changes to the base layer. While our work extends beyond Ethereum and EVM chains, showing that this is possible on Ethereum today implies that the most used smart-contract ecosystem can be augmented with confidential smart contracts.
• Outside the context of blockchains, our solution can be seen as a more efficient (cryptoeconomic) solution to the problem of verifiable FHE.
1.2 Related Work
Our work builds upon the existing body of research and development of confidential smart contract platforms. Unlike all other works, to the best of our knowledge we are the first to describe a solution that operates fully and natively as a L2. More specifically, other confidential smart contract platforms usually differ by the kinds of privacy-preserving technologies they use:
• Trusted Execution Environment (TEEs) Based. Currently, the only confidential smart contracts networks in production are using TEEs (or secure enclaves) [13, 29, 38, 47]. These networks simulate secure computation by allowing users to encrypt their transactions with keys held inside of a secure enclave. Transactions then get decrypted and executed inside of the enclave, which ensures confidentiality as long as we can trust the security of the TEE. While TEEs are by far the most efficient solution, they are susceptible to side-channel attacks and other vulnerabilities (e.g., [7, 12, 42]).
• Secure Multiparty Computation (MPC) Based. Since our work relies on Threshold FHE, we share a similar threat model with these works (e.g., [2–4, 20, 48, 49]). However, for the purpose of presentation, we separate these from FHE-based solutions, as they often rely on linear secret-sharing [5, 21] and garbled circuits techniques [46]. The main drawback in these techniques compared to our work is that MPC protocols need to communicate data proportional to the circuit size in order to evaluate it. In the case of secret-sharing-based MPC, all parties also need to sequentially communicate with all other parties any time they evaluate a multiplication gate. In the context of public blockchains, this is impractical, as the latency is quite high and the bandwidth is limited. Furthermore, as these systems require multiple interacting nodes for every contract execution, they are not amenable to a rollup architecture such as the one we are proposing.
• ZK-based. Different works have considered confidential smart contracts using different ZK schemes. However, since ZK techniques are more suitable for verifiable computation (e.g., [34]), their utility for confidential smart contracts is limited. To overcome this, Hawk [28] suggested having a data-manager – an off-chain party that is tasked with collecting inputs from different clients and is trusted with seeing everyone’s data. Alternatively, other platforms impose limitations on developers [8, 9, 24, 45].
• FHE-based. In the last couple of years, as a result of significant FHE performance improvements, HE and FHE based solutions have started to emerge [1, 16, 39–41]. These platforms are closest to our work, but none of them adopt a rollup architecture, which limits their scalability in practice. Some of these works adopt a Threshold FHE structure as we do (e.g., [1]), whereas others such as [40] allow limited functionality, but without a shared global encryption key-pair.
2 Preliminaries
2.1 Rollups Rollups are a scaling solution designed to alleviate the congestion on the primary L1 chain, in particularly Ethereum. With Ethereum’s growing user base, the need for scaling solutions has become paramount. The primary goal of scalability is to enhance transaction speed and throughput without compromising on decentralization or security. Rollups execute transactions outside the base layer, posting back state-updates alongside proofs of correct execution. Ultimately, the L1 (Ethereum in our case) reaches consensus on these state updates, but it does so without re-executing the transactions on the base layer. In other words, transactions on the L2 rollup are secured by Ethereum’s inherent security. There are two main types of Rollups, which differ by how proofs are created and verified:
• Optimistic Rollups. These assume transactions are valid unless challenged. They move computation offchain but post transaction data to Ethereum, allowing anyone to re-run the transactions off-chain and verify for themselves that the execution is correct. If any verifier detects malicious behavior, they can submit a fraud-proof on-chain, in which case the L1 acts as the final arbiter. For this reason, Optimistic Rollups require a dispute period (often of a few days).
• ZK Rollups. These rollups similarly execute contracts off-chain and submit validity proofs back when sending a state-update. Validity proofs are constructed using advanced cryptographic techniques known as (succinct) ZK Proofs. They can be efficiently verified on-chain directly, without posting the full transaction data or having a dispute period.
Optimistic and ZK Rollups have inherently different trade-offs. Optimistic rollups suffer from a dispute-period delay, making finality longer. They also require posting the transactions themselves on-chain, which negates some of the scalability benefits 2.
On the other hand, ZK Rollups require significant computation power (and time) to produce a proof, especially the closer you try to get to native EVM [10]. A related downside is that these rollups are much more complicated to build, resulting in large amounts of code. The likelihood of critical vulnerabilities with zkEVMs is therefore much higher, at least until they have been battle tested enough over time.
2.1.1 Optimistic Rollups in More Detail.
Optimistic rollups bundle multiple off-chain transactions and submit them to the L1 chain, reducing costs for users. They are termed “optimistic” because they assume transactions are valid unless proven otherwise. If a transaction is challenged, a fraud proof is computed. If proven fraudulent, penalties are applied. Today, optimistic rollups operate atop Ethereum, managed by Ethereum-based smart contracts. They process transactions off-chain but post data batches to an on-chain rollup contract. Ethereum ensures the correctness of rollup computations and handles data availability, making rollups more secure than standalone off-chain solutions or sidechains. They also create an inherent economic-security alignment between the two layers, as the L2 receives security while paying for incurred fees at the L1 level.
From an architectural perspective, optimistic rollups consist of the following:
• Transaction Execution. Users send transactions to operators or validators, who aggregate and compress them for the L1.
• Submitting to the L1. Operators bundle transactions and send them to the L1 using calldata.
• State Commitments. The rollup’s state is represented as a Merkle tree. Operators submit old and new state roots, ensuring the chain’s integrity.
• Fraud Proofs and Disputes. These allow anyone to challenge a transaction’s validity. If a challenge is valid (arbitrated by the L1), the fraudulent party is penalized.
Fraud Proofs play a vital role in optimistic rollups, and they are at the root of how we ensure that a rollup publishes a correct state update. Even in the face of malicious nodes trying to delay or tamper with transactions, the chain’s integrity is preserved as long as there’s a single honest node that observes state updates and checks that they are correct. In the context of rollups built on Ethereum, because the
actual data is posted onto Ethereum, anyone in the world canact as a verifier. Once an honest verifier detects an incorrect state update (e.g., by including a tampered-with transaction), it can submit a dispute, which initiates the fraud proof game: a multi-round interactive protocol. Here, the asserter (the node that produced the state update) and challenger (the verifier who issued a dispute) follow a protocol overseen by an L1 verifier contract to ascertain the honest party. The protocol proceeds recursively, each time dividing the computation into two equal parts. The challenger chooses one part to challenge each time. This process, termed the bisection protocol, persists until only one computational step is in question. Once the interactive protocol narrows down to a single instruction, it is the L1 contract’s turn to resolve the dispute by evaluating the instruction result as well as both the asserter’s and the challenger’s claims and their respective results to determine which one is correct.
2.2 Fully Homomorphic Encryption (FHE).
Fully Homomorphic Encryption (FHE) enables computations on ciphertexts that, when decrypted, match the results of those operations as if they were performed on the plaintext directly.
In practice, ever since the original scheme by Gentry [19], several FHE schemes have been developed, which are based on the original Learning With Errors (LWE) hardness problem, or related algebraic constructs such as its ring variant [37]. Our implementation utilizes a scheme called TFHE [14], but as the scheme itself does not really matter for the purpose of constructing an FHE-rollup, we describe FHE more generally below, in a black-box manner.
A generic FHE scheme can be denoted by the tuple of algorithms FHE = (Gen, Enc, Dec, Eval), as follows:
• Gen(1 𝜅 ). Given a security parameter 1 𝜅 , the algorithm outputs a pair of keys (𝑝𝑘, 𝑠𝑘) where 𝑝𝑘 is the public encryption key and 𝑠𝑘 is the secret decryption key. Define domains P for plaintexts, R for randomness, and C for ciphertexts, as well as the set of permissible functions F.
• Enc(𝑝𝑘,𝑚;𝑟). Given the public key 𝑝𝑘, a message 𝑚 ∈ P and randomness 𝑟 ∈ R, the encryption algorithm produces a ciphertext 𝑐 ∈ C such that
𝑐 = Enc𝑝𝑘 (𝑚;𝑟).
• Dec(𝑠𝑘, 𝑐). With the secret key 𝑠𝑘 and a ciphertext 𝑐, the decryption algorithm retrieves the original plaintext message 𝑚:
𝑚 = Dec𝑠𝑘 (𝑐).
• Eval(𝑝𝑘, 𝑓 , {𝑐𝑖 } 𝑛 𝑖=1 ). Given the public key 𝑝𝑘, a function 𝑓 ∈ F, and a set of ciphertexts {𝑐𝑖 } 𝑛 𝑖=1 , this algorithm produces a ciphertext 𝑐 ′ ∈ C such that:
Dec𝑠𝑘 (𝑐 ′ ) = 𝑓 ({Dec𝑠𝑘 (𝑐𝑖)}𝑛 𝑖=1 ).
_____________________________________
2This is meant to be mitigated to an extent with EIP-4844 and Danksharding.
This implies the function 𝑓 is executed over encrypted data, and its result is
encrypted as 𝑐 ′.
3 Architecture
3.1 FHE Rollups: Optimistic or ZK-based?
As mentioned, ZK Rollups are inherently slower on the proving-side, but this provides benefits on the verification side. This problem compounds when considering ZK in the context of FHE, as we are now essentially combining two heavy-duty cryptographic techniques together. While an increasing body of work looks to address this research gap, current proposed solutions are orders of magnitude slower [11, 43]. For this reason, using an optimistic-based approach becomes a more natural choice for the encrypted domain.
3.2 Design Overview and Implementation Details
Our platform is built with modularity in mind. It includes the quintessential components of a rollup, encompassing a sequencer, prover, and a DA layer, whilst simultaneously interweaving new and specific components needed to support an FHE Rollup. Figure 4 illustrates the overall design. We detail the new FHE rollup-specific components below.
3.3 fheOS
The core FHE logic sits in our fheOS library. It is an encrypted computation library of pre-compiles for common encrypted opcodes, such as comparing two numbers and doing arithmetic operations like addition and multiplication. It gives Smart Contracts running on the network the ability to use FHE primitives within the contract. That means that dApps running on (or using) Fhenix will be able to integrate encrypted data in their smart contract logic. Developers will have the choice to decide what will be encrypted and what will remain plaintext. fheOS is another EVM-friendly wrapper around Zama’s tfhe-rs 3 FHE libraries, similar to fhEVM [1]. For implementation purposes and modularity, we opted to design our own version.
The fheOS library is the core engine of the Fhenix node; smart contracts utilizing encryption features will call fheOS precompiles for common FHE operations, and fheOS itself will be responsible for communication and authentication between the rollup and the Threshold Services Network (TSN, see Section 4) for decryption and re-encryption requests while proving that the decryption request is legitimate.
The fheOS library is designed to be injected as an extension into any existing flavor of EVM, meaning that it is fully EVM-compatible, thus keeping all the existing EVM functionality in place while boosting developers’ ability to explore new use cases.
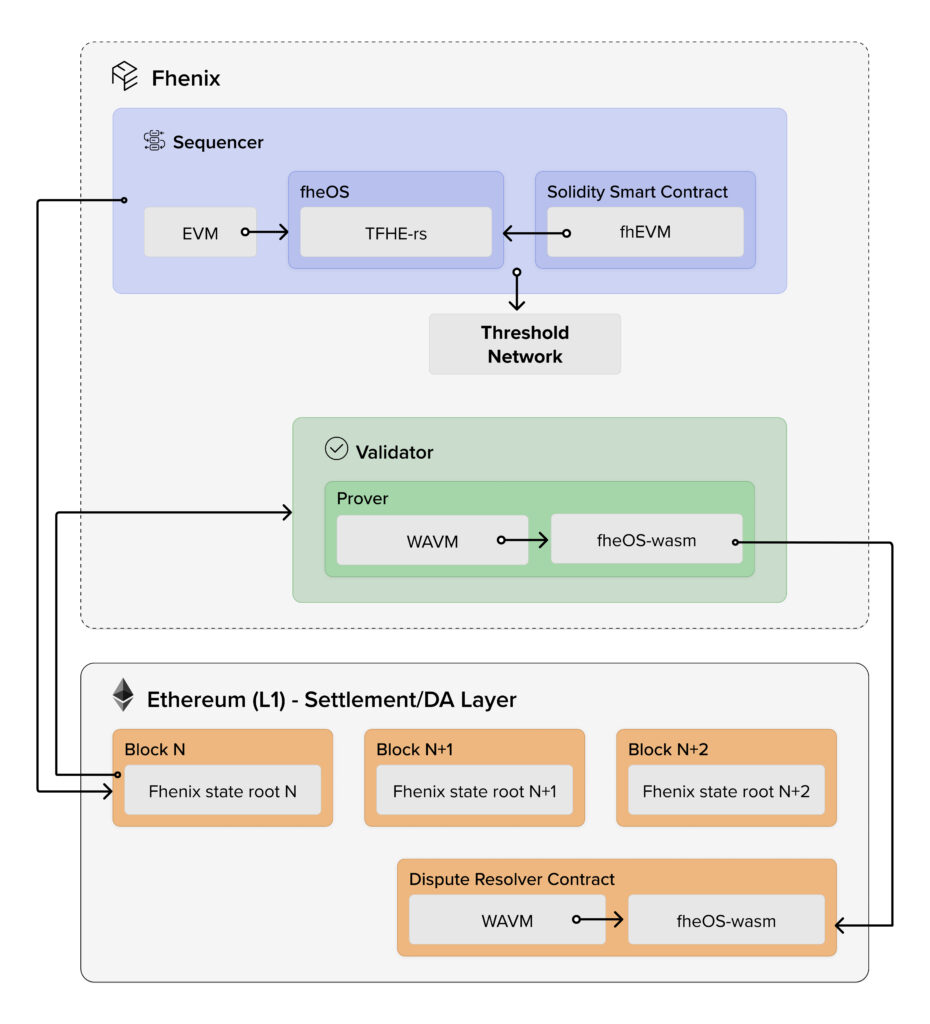
Figure 1. Overview of an FHE Rollup architecture
3.4 go-tfhe
As we sought to extend the capabilities of Ethereum’s goethereum (geth), their predominant client written in Go, we encountered a challenge: the core FHE mathematical operations library, tfhe-rs, is written in Rust, necessitating communication via a foreign function interface (FFI). To address this, we developed go-fhe, which encompasses:
1. Go-based API. This component provides all essential interfaces for executing FHE mathematical operations using Go. It serves as the primary point of interaction for blockchain developers familiar
with Go.
2. Rust Wrapper for TFHE.rs. We created a specialized wrapper that adapts the TFHE.rs library functions for blockchain applications.
3. FFI Integration between Go API and the Rust Wrapper. To bridge the two languages, our interface employs cgo and extern “C” mechanisms. This facilitates bindings between Golang and Rust, aligning function calls, types, and naming conventions.
_________________________________________
3https://github.com/zama-ai/tfhe-rs
In general, go-tfhe acts as a modular extensionable lightweight bridge between tfhe-rs and the blockchain application.
4 Threshold Services Network (TSN)
A key component in our design is the Threshold Services Network (TSN). This network is separate from the L1 or other rollup components and plays several key roles. In particular, this network is collectively entrusted with the secret-shared network key [𝑠𝑘], which can be used for threshold decryption. Our current implementation utilizes [15], which uses Shamir secret-sharing to split 𝑠𝑘 into 𝑛 shares, out of which 𝑡 + 1 shares are needed to reconstruct. In practice, each bit is separately shared, but we will ignore that distinction for the purpose of this paper.
4.1 Threshold Decryption and Re-encryption Occasionally, the network will need to decrypt certain results, or re-encrypt them to a designated user. The TSN is incharge of any such request coming from the rollup, and can accommodate it using the threshold decryption protocol of [15].
To illustrate why this is needed, consider the following two examples. First, imagine a private voting contract deployed on the rollup. When users vote for a certain candidate, they encrypt their votes, and the contract tallies these votes (all encrypted). At a certain point in time, a functionality in the contract should be able to decrypt the tally and announce the winner. This request is routed to the TSN, which decrypts it and returns the result to be stored in the contract’s state. This flow is illustrated in Figure 2, and a snippet from the Solidity contract code appears in Figure 3.
A similar example is that of a user who owns a NFT with private metadata only they can see. Such metadata is stored in the contract’s state under the network’s key. When a user tries to access that information, the contract should threshold re-encrypt it so only the designated user would be able to decrypt and get access to the underlying data.
4.2 Proofs on Secret Shared Data In certain cases, we might be able to leverage the TSN to assist in proving important statements about the data being encrypted [6]. For example, it is a well-established fact that ciphertexts need to be well-formed, otherwise trying to decrypt malformed ciphertexts could leak information about the secret key [27]. Similarly, in a multi-user system such as this, we need to ensure that a user is not (for example) sending a ciphertext they did not encrypt, and are asking the TSN to decrypt it for them. For these reasons, whenever a user submits an encrypted input, we need to ensure it has been properly encrypted and that the user knows the underlying plaintext.
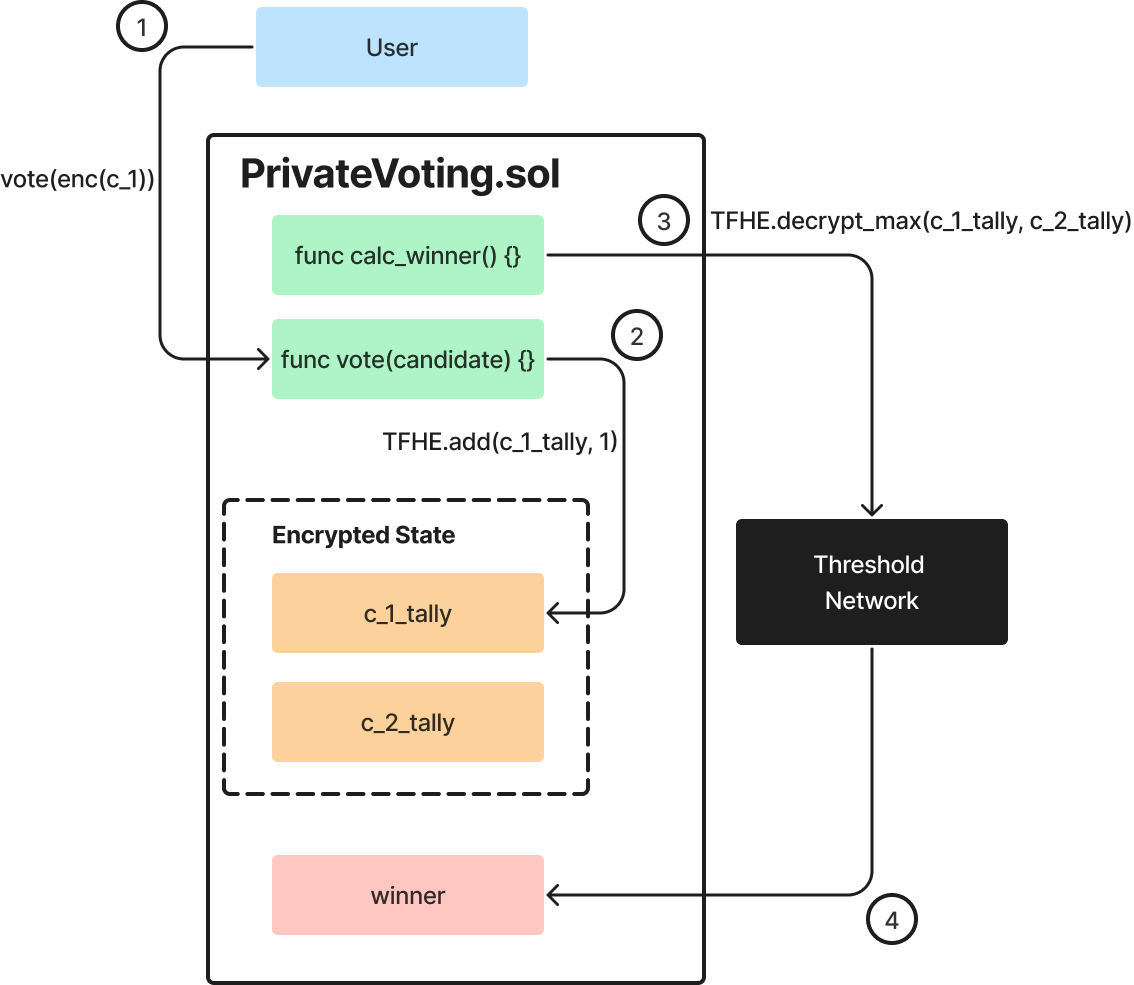
Figure 2. Smart contract request to decrypt FHE-encrypted data on Fhenix
Currently, state of the art zero-knowledge proofs of knowledge (ZKPoK) over FHE ciphertexts [30] are still relatively expensive, and would add a non-trivial amount of overhead to each transaction. One alternative would be to have clients start by secret-sharing their secret inputs to the TSN using a verifiable secret-sharing protocol (VSS) [18]. After confirming that the inputs have been properly secret-shared, the network can jointly encrypt the inputs, for example, by the following simplified protocol sketch.
• Protocol ThresholdEncryption. Given a shared user message [𝑚], and a pre-processed randomness tuple ( [𝑟], 𝐸𝑛𝑐𝑝𝑘 (𝑟)) the parties output the FHE ciphertext 𝑐𝑡 := 𝐸𝑛𝑐𝑝𝑘 (𝑚).
• The servers run a VSS protocol with the client, receiving and validating the sharing of [𝑚].
• The servers jointly reconstruct 𝑐 := 𝑂𝑝𝑒𝑛( [𝑚] − [𝑟]) using an actively secure MPC protocol
• Output 𝑐𝑡 := 𝐸𝑛𝑐𝑝𝑘 (𝑟) + 𝐸𝑛𝑐𝑝𝑘 (𝑐).
* Note that since 𝑐𝑡 is a public value that is a result of secure sequential protocols, the parties can reach consensus over it to ensure correctness.
4.3 Random Beacon
A uniquely necessary functionality for smart contracts is that of producing randomness. Smart contracts are inherently deterministic, so they need an external source of randomness

Figure 3. Example FHE Voting Contract in Solidity
to enable non-deterministic functionalities. Examples of usecases that require such functionality are on-chain gaming (e.g., Poker, Casinos), NFT mints, and others.
Many distributed coin-tossing protocols exist. One such example that is well-fitted to our case is the one based on Verifiable Random Functions (VRF) [32] in [33].
4.4 Secure Shuffle
In many cases, we need a functionality dedicated to shuffling a vector of inputs. Many privacy-preserving computation techniques, including those that leverage FHE, can benefit from an efficient secure shuffle primitive. There are countless of examples where shuffling comes into play. One simple example is a game of poker – where securely and privately shuffling the deck is crucial.
More importantly, secure shuffles are a critical building block for Oblivious RAM (ORAM) [22], which are schemes that ensure that the memory is not just encrypted, but also that all accesses to it are kept private. Using an ORAM could be a building block into constructing a more efficient fhEVM that allows running FHE computations over programs directly, without first unrolling them into circuits [17, 44]. Other applications such as building private search engines [23], or building truly anonymous tokens in the account based model require a form of ORAM [25].
4.5 Security
It is important to note that the underlying confidentiality guarantees of the entire system are closely related to the trust assumptions of the TSN. Anything that relates to keeping the threshold decryption key safe, correctly decrypting/reencrypting ciphertexts, etc., is under the responsibility of the TSN.
Currently, the state-of-the-art protocols by [15] require the TSN to have at most 𝑡 < 𝑛 3 malicious corruptions for a fast and robust protocol, or 𝑡 < 𝑛 2 if we are willing to settle for security with abort.
4.5.1 Proposed Improvements (and Open Future Research). We put forward several open research areas we plan to explore regarding the TSN and its current threshold decryption protocol. We invite the community to join us in advancing these topics of interest:
• An actively secure threshold decryption protocol supporting a dishonest majority
• Cheater identification – for the protocol supporting up to 𝑡 < 𝑛 2 corruptions (or any dishonest majority protocol) we should be able to identify a cheating party (whether one that subverts the protocol, or one that aborts). Without it, there is no way to prevent Denialof-Service attacks on the TSN.
• Many validators (>1000) through sampling – currently the schemes do not scale well enough to many validators. This is especially true for the one limited to 𝑡 < 𝑛 3 , which has a computational complexity that increases exponentially with (𝑡, 𝑛). One solution to this problem is to focus on sampling a small committee for each epoch [20, 49].
• Share rotation and recovery. Many such schemes are already present in the literature (e.g., [31]).
5 Fraud Proofs
The key to Optimistic Rollups lies in their fraud proofs mechanism. But how do we fit that mechanism, in particular Ethereum’s EVM, to work with smart contracts that execute FHE circuits over encrypted data?
First, observe that FHE, unlike other encrypted computation techniques such as MPC, natively allows anyone to verify that a computation was done correctly, without breaking the privacy guarantees. This is because an adversary holding the encrypted inputs and outputs learns nothing about the underlying encrypted data (if this were not the case, then the encryption scheme would not be semantically secure).
This makes verifying FHE computations compatible with the idea of Optimistic Rollups, at least in theory. As mentioned earlier, Optimistic Rollups are based on posting the full transaction data on the L1 (or some other data availability service), alongside the output. In this case, both are encrypted. Just like with plaintext data, any off-chain verifier could take the encrypted transaction data, re-execute the transactions, and make sure that they receive the same encrypted output. If this is not the case, then an honest verifier could submit a dispute and start the arbitration process with the L1.
However, the whole fraud proving mechanism is rooted on the L1’s ability to determine unequivocally whether the L2 node that posted the state update or the disputing verifier (i.e., the challenger) is cheating. To do this, the L1 needs to be able to run a single computational step of the underlying computation. Since we are interested in Ethereum being the L1, this poses a question: How can Ethereum, or any traditional EVM chain, validate execution on FHE primitives without inherent support for FHE operations?
The answer resides in Arbitrum’s Nitro fraud prover 4 , which we repurpose to our needs, allowing us to compile all our FHE logic to WebAssembly and execute the entire proving round in a WASM runtime (WAVM), on-chain on Ethereum, instead on native EVM. Since the underlying FHE code can be compiled to WASM as well, no changes are needed to the L1 itself.
Addressing performance concerns, it is rational to assume that if FHE computations are inherently intensive, simulating them in a WASM runtime atop EVM might incur significant performance penalties. While this is a valid concern, it is important to remember that initiating these computations is only mandatory in a dispute scenario, and real-time speed is not an absolute necessity given a sufficient dispute window. Considering that the standard practice allocates approximately seven days for it, we estimate that this is more than sufficient time to settle any such disputes. However, we did not empirically validate this hypothesis, and we note that doing so in the future is important.
5.1 Implementation details
During the course of developing the proof-of-concept FHE fraud prover, we had to overcome several hurdles, which we note here for completeness.
First, To run go-tfhe as a part of the fraud proof mechanism, it was necessary to adapt the code for execution in WebAssembly (WASM). Given our reliance on FHE code written in Rust, while much of blockchain code is traditionally in Golang, we faced challenges in native compilation to a unified WASM module – the default bindings between Rust and Golang use cgo, which is not compatible with WASM. To address this, we crafted bindings in WASM
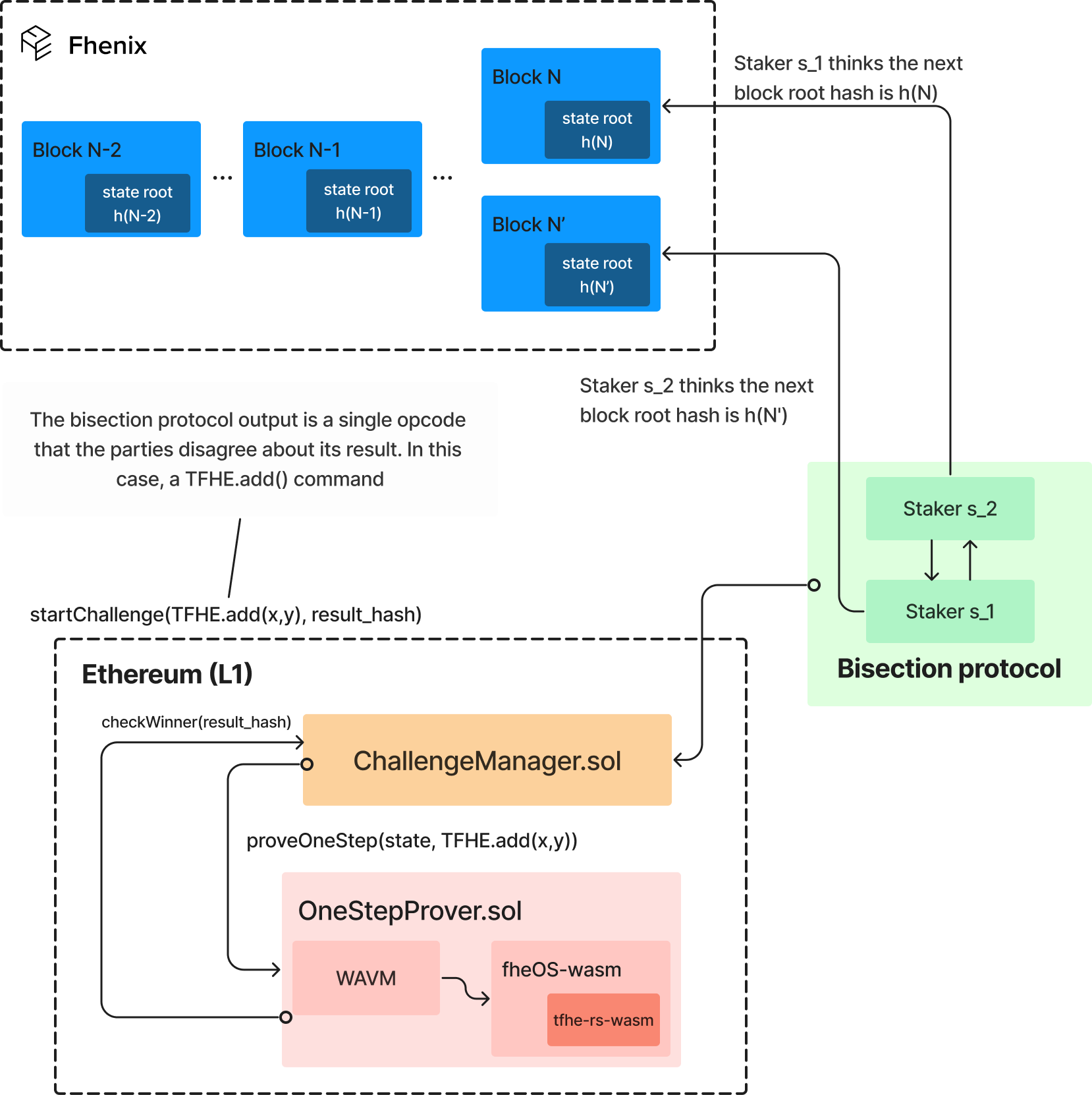
Figure 4. Fraud proof engine for FHE instructions
to bridge between Golang, using the mainline Golang compiler’s external function directives, and Rust, creating a dedicated Rust file as the primary WASM build target, eventually linking both using wasm-merge for a cohesive .wasm output.
Furthermore, we had to modify tfhe-rs as well. At the time of this writing, tfhe-rs supports compilation and execution of WASM in browsers only. In our case – smart contracts running atop of a blockchain – the interfaces available differ from those of browser contexts. Notably, some API calls, such as accessing operating-system capabilities or multithreading, are not accessible. For TFHE.rs to be compatible with a smart contract context, two primary modifications were made:
1. Disabling Multithreading. Given that most smart contracts do not accommodate multithreading or concurrency, the code was adjusted to operate in a single-threaded and deterministic manner.
2. Custom Random Number Provider Integration. The initial version of tfhe.rs depended on predefined random number providers or seeders. The only available seeders were contingent on the operating system’s ability to generate random numbers. We introduced a custom seeder managed by the library user. This seeder receives an input seed and passes it into a ChaCha20-based seeded Pseudorandom Number Generator (PRNG) provider. This modification negates the need for non-deterministic random numbers in the FHE implementation, facilitating external validation by replicating computations using consistent inputs from blockchain data and state.
We note that based on our benchmarks of tfhe-rs running in this context show an order of magntitude performance degradation when using wasmer/cranelift and 8x when using wasmer/llvm for add operations (tested on i9-13900K, 128 GB RAM, wasmer 4.0). We note that the Arbitrum fraud proof engine makes use of software floating points which should impact performance further, but we did not complete benchmark tests as of writing this paper.
6 Conclusion
In this paper, we presented the first proposed construct of an FHE Rollup, a novel solution that adds confidentiality to Ethereum and other EVM chains. Our approach leverages the power of FHE to enable encrypted EVM computations, revolutionizing the way transactions are executed and confidential data is handled on-chain. Unlike recent works [1, 16, 39], our approach uses a L2 Rollup structure to avoid replicating the cost of FHE computations across all nodes, which leads to a much more efficient and practical solution.
Our approach focuses on Ethereum and the EVM, but is also of independent value as a system that enables verifiable FHE [43]. Additionally, we also laid out the architecture of our proposed FHE rollup system, including its components and layers, and have proposed and implemented a proof-ofconcept of a fraud-proof solution that requires no changes whatsoever to Ethereum. Our work contributes to the development of a new wave of privacy-centric decentralized applications, enhancing user confidence, expanding potential use-cases, and increasing the overall security and utility of the Ethereum network.
References
[1] Zama AI. 2023. FHEVM Whitepaper. https://github.com/zama-ai/ fhevm/blob/main/fhevm-whitepaper.pdf. Accessed: 27-10-2023.
[2] Aritra Banerjee, Michael Clear, and Hitesh Tewari. 2021. zkhawk: Practical private smart contracts from mpc-based hawk. In 2021 3rd Conference on Blockchain Research & Applications for Innovative Networks and Services (BRAINS). IEEE, 245–248.
[3] Carsten Baum, James Hsin-yu Chiang, Bernardo David, and Tore Kasper Frederiksen. 2022. Eagle: Efficient Privacy Preserving Smart Contracts. Cryptology ePrint Archive (2022).
[4] Carsten Baum, Bernardo David, and Rafael Dowsley. 2020. Insured MPC: Efficient secure computation with financial penalties. In Financial Cryptography and Data Security: 24th International Conference, FC 2020, Kota Kinabalu, Malaysia, February 10–14, 2020 Revised Selected Papers 24. Springer, 404–420.
[5] Michael Ben-Or, Shafi Goldwasser, and Avi Wigderson. 1988. Completeness theorems for non-cryptographic fault-tolerant distributed computation. In Proceedings of the twentieth annual ACM symposium on Theory of computing. ACM, 1–10.
[6] Dan Boneh, Elette Boyle, Henry Corrigan-Gibbs, Niv Gilboa, and Yuval Ishai. 2019. Zero-knowledge proofs on secret-shared data via fully linear PCPs. In Annual International Cryptology Conference. Springer, 67–97.
[7] Pietro Borrello, Andreas Kogler, Martin Schwarzl, Moritz Lipp, Daniel Gruss, and Michael Schwarz. 2022. {ÆPIC} Leak: Architecturally Leaking Uninitialized Data from the Microarchitecture. In 31st USENIX Security Symposium (USENIX Security 22). 3917–3934.
[8] Sean Bowe, Alessandro Chiesa, Matthew Green, Ian Miers, Pratyush Mishra, and Howard Wu. 2020. Zexe: Enabling decentralized private computation. In 2020 IEEE Symposium on Security and Privacy (SP). IEEE, 947–964.
[9] Benedikt Bünz, Shashank Agrawal, Mahdi Zamani, and Dan Boneh. 2020. Zether: Towards privacy in a smart contract world. In Financial Cryptography and Data Security: 24th International Conference, FC 2020, Kota Kinabalu, Malaysia, February 10–14, 2020 Revised Selected Papers. Springer, 423–443.
[10] Vitalik Buterin. 2022. zkEVM and zkRollup. https://vitalik.ca/general/ 2022/08/04/zkevm.html. Accessed: dd-mm-yyyy.
[11] Sylvain Chatel, Christian Mouchet, Ali Utkan Sahin, Apostolos Pyrgelis, Carmela Troncoso, and Jean-Pierre Hubaux. 2023. PELTA– Shielding Multiparty-FHE against Malicious Adversaries. Cryptology ePrint Archive (2023).
[12] Guoxing Chen, Sanchuan Chen, Yuan Xiao, Yinqian Zhang, Zhiqiang Lin, and Ten H Lai. 2019. Sgxpectre: Stealing intel secrets from sgx enclaves via speculative execution. In 2019 IEEE European Symposium on Security and Privacy (EuroS&P). IEEE, 142–157.
[13] Raymond Cheng, Fan Zhang, Jernej Kos, Warren He, Nicholas Hynes, Noah Johnson, Ari Juels, Andrew Miller, and Dawn Song. 2019. Ekiden: A platform for confidentiality-preserving, trustworthy, and performant smart contracts. In 2019 IEEE European Symposium on Security and Privacy (EuroS&P). IEEE, 185–200.
[14] Ilaria Chillotti, Nicolas Gama, Mariya Georgieva, and Malika Izabachène. 2020. TFHE: fast fully homomorphic encryption over the torus. Journal of Cryptology 33, 1 (2020), 34–91.
[15] Morten Dahl, Daniel Demmler, Sarah El Kazdadi, Arthur Meyre, JeanBaptiste Orfila, Dragos Rotaru, Nigel P Smart, Samuel Tap, and Michael Walter. 2023. Noah’s Ark: Efficient Threshold-FHE Using Noise Flooding. Cryptology ePrint Archive (2023).
[16] Wei Dai. 2022. Pesca: A privacy-enhancing smart-contract architecture. Cryptology ePrint Archive (2022).
[17] Jack Doerner and Abhi Shelat. 2017. Scaling ORAM for secure computation. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. 523–535.
[18] Paul Feldman. 1987. A practical scheme for non-interactive verifiable secret sharing. In 28th Annual Symposium on Foundations of Computer Science (sfcs 1987). IEEE, 427–438.
[19] Craig Gentry. 2009. Fully homomorphic encryption using ideal lattices. In Proceedings of the forty-first annual ACM symposium on Theory of computing. 169–178.
[20] Craig Gentry, Shai Halevi, Hugo Krawczyk, Bernardo Magri, Jesper Buus Nielsen, Tal Rabin, and Sophia Yakoubov. 2021. YOSO: You Only Speak Once: Secure MPC with Stateless Ephemeral Roles. In Advances in Cryptology–CRYPTO 2021: 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, August 16–20, 2021, Proceedings, Part II. Springer, 64–93.
[21] Oded Goldreich, Silvio Micali, and Avi Wigderson. 1987. How to play any mental game. Proceedings of the nineteenth annual ACM symposium on Theory of computing (1987), 218–229.
[22] Oded Goldreich and Rafail Ostrovsky. 1996. Software protection and simulation on oblivious RAMs. Journal of the ACM (JACM) 43, 3 (1996), 431–473.
[23] Alexandra Henzinger, Emma Dauterman, Henry Corrigan-Gibbs, and Nickolai Zeldovich. 2023. Private web search with Tiptoe. Cryptology ePrint Archive (2023).
[24] Aleo Systems Inc. 2022. Aleo: A Zero-Knowledge Operating System. https://aleo.org/. Accessed: dd-mm-yyyy.
[25] Nerla Jean-Louis, Yunqi Li, Yan Ji, Harjasleen Malvai, Thomas Yurek, Sylvain Bellemare, and Andrew Miller. 2023. SGXonerated: Finding (and Partially Fixing) Privacy Flaws in TEE-based Smart Contract Platforms Without Breaking the TEE. Cryptology ePrint Archive (2023).
[26] Harry Kalodner, Steven Goldfeder, Xiaoqi Chen, S Matthew Weinberg, and Edward W Felten. 2018. Arbitrum: Scalable, private smart contracts. In 27th USENIX Security Symposium (USENIX Security 18). USENIX Association, 1353–1370. https://www.usenix.org/conference/ usenixsecurity18/presentation/kalodner Accessed: dd-mm-yyyy.
[27] Mehmet Kiraz and Berry Schoenmakers. 2006. A protocol issue for the malicious case of Yaoâs garbled circuit construction. In 27th Symposium on Information Theory in the Benelux, Vol. 29. 283–290.
[28] Ahmed Kosba, Andrew Miller, Elaine Shi, Zikai Wen, and Charalampos Papamanthou. 2016. Hawk: The blockchain model of cryptography and privacy-preserving smart contracts. In 2016 IEEE symposium on security and privacy (SP). IEEE, 839–858.
[29] Rujia Li, Qin Wang, Qi Wang, David Galindo, and Mark Ryan. 2022. SoK: TEE-assisted confidential smart contract. arXiv preprint arXiv:2203.08548 (2022).
[30] Benoit Libert. 2023. Vector Commitments With Short Proofs of Smallness. Cryptology ePrint Archive (2023).
[31] Sai Krishna Deepak Maram, Fan Zhang, Lun Wang, Andrew Low, Yupeng Zhang, Ari Juels, and Dawn Song. 2019. CHURP: dynamiccommittee proactive secret sharing. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. 2369– 2386.
[32] Silvio Micali, Michael Rabin, and Salil Vadhan. 1999. Verifiable random functions. In 40th annual symposium on foundations of computer science (cat. No. 99CB37039). IEEE, 120–130.
[33] League of Entropy. 2022. drand: Distributed Randomness Beacon. https://drand.love/. Accessed: 27-10-2023.
[34] Bryan Parno, Jon Howell, Craig Gentry, and Mariana Raykova. 2013. Pinocchio: Nearly practical verifiable computation. In 2013 IEEE Symposium on Security and Privacy. IEEE, 238–252.
[35] Optimism PBC. 2022. Optimism: Optimistic Ethereum. https:// optimism.io/. Accessed: 27-10-2023.
[36] Joseph Poon and Vitalik Buterin. 2017. Plasma: Scalable Autonomous Smart Contracts. https://plasma.io/plasma.pdf. Accessed: dd-mmyyyy.
[37] Oded Regev. 2009. On lattices, learning with errors, random linear codes, and cryptography. Journal of the ACM (JACM) 56, 6 (2009), 1–40.
[38] SCRT. 2021. The Secret Network Graypaper. https://scrt.network/ graypaper.
[39] Ravital Solomon and Ghada Almashaqbeh. 2021. smartfhe: Privacypreserving smart contracts from fully homomorphic encryption. Cryptology ePrint Archive (2021).
[40] Samuel Steffen, Benjamin Bichsel, Roger Baumgartner, and Martin Vechev. 2022. Zeestar: Private smart contracts by homomorphic encryption and zero-knowledge proofs. In 2022 IEEE Symposium on Security and Privacy (SP). IEEE, 179–197.
[41] Samuel Steffen, Benjamin Bichsel, Mario Gersbach, Noa Melchior, Petar Tsankov, and Martin Vechev. 2019. zkay: Specifying and enforcing data privacy in smart contracts. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security. 1759–1776.
[42] Stephan Van Schaik, Andrew Kwong, Daniel Genkin, and Yuval Yarom. 2020. SGAxe: How SGX fails in practice. https://sgaxe.com/files/ SGAxe.pdf
[43] Alexander Viand, Christian Knabenhans, and Anwar Hithnawi. 2023. Verifiable fully homomorphic encryption. arXiv preprint arXiv:2301.07041 (2023).
[44] Xiao Wang, Hubert Chan, and Elaine Shi. 2015. Circuit oram: On tightness of the goldreich-ostrovsky lower bound. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. 850–861.
[45] Zachary J Williamson. 2018. The aztec protocol. URL: https://github. com/AztecProtocol/AZTEC (2018).
[46] Andrew C Yao. 1986. How to generate and exchange secrets. In 27th Annual Symposium on Foundations of Computer Science (sfcs 1986). IEEE, 162–167.
[47] Hang Yin, Shunfan Zhou, and Jun Jiang. 2019. Phala network: A confidential smart contract network based on polkadot.
[48] Guy Zyskind, Oz Nathan, et al. 2015. Decentralizing privacy: Using blockchain to protect personal data. In 2015 IEEE Security and Privacy Workshops. IEEE, 180–184.
[49] Guy Zyskind, Oz Nathan, and Alex Pentland. 2015. Enigma: Decentralized computation platform with guaranteed privacy. arXiv preprint arXiv:1506.03471 (2015).



